Mostrar el código
library(tidyverse)
library(readxl)
library(patchwork)
library(ggview)
library(ggrepel)
library(gtsummary)
library(gt)
library(ggpmisc) # Para agregar la ecuación de la recta a cada faceta
library(broom)
library(sessioninfo)
Primero cargo las librerías:
Y luego cargo la base de datos, la limpio y edito:
Mostrar el código
cobres_nueva <- read_excel("ANPP_Precipitaciones Oct Marz.xlsx", sheet = "Cobres_R") # esta es la nueva, con precipitaciones extrapoladas
cobres_nueva <- cobres_nueva %>%
mutate(
sitio2 = factor(sitio, labels = c("Estepa\narbustiva", "Estepa\nherbácea/arbustiva"))
)1 Precipitaciones
Los siguientes análisis los hago con las precipitaciones estimadas de Gaitán y Biancari (2024), método 2. En promedio, por cada estación de crecimiento (de octubre a marzo), las precipitaciones fueron de 150.27 mm, con una variabilidad relativamente baja (CV = 18%), en comparación a la variabilidad en la PPAN.
Mostrar el código
cobres_nueva %>%
filter(sitio == "Campo") %>%
summarise(
media = round(mean(precip_gaitan_2, na.rm = T),2),
sd = round(sd(precip_gaitan_2, na.rm = T),2),
CV = round(sd/media*100,2),
min = round(min(precip_gaitan_2, na.rm = T),2),
max = round(max(precip_gaitan_2, na.rm = T),2)
) %>%
gt()| media | sd | CV | min | max |
|---|---|---|---|---|
| 150.27 | 26.98 | 17.95 | 117.66 | 207.49 |
2 PPAN en ambos sitios ecológicos
Como el artículo apunta a un público amplio, que no necesariamente conocen la puna ni sus ambientes, nos conviene llamar a los sitios ecológicos de una manera más general, usando la fisonomía y estructura. El Cerro corresponde a una Estepa herbáceo/arbustiva en relieves escarpados y el Campo a una Estepa arbustiva en planicie. En los gráficos usé esas nuevas denominaciones, un poco más acortados.
2.1 Análisis descriptivo
Resumo la PPAN para ambos tipos de estepas con un gráfico de cajas, mostrando además la media aritmética y los datos de PPAN de cada año (puntos grises).
Mostrar el código
# Calculamos las medias de PPAN por sitio
# medias_ppna <- cobres_nueva %>%
# group_by(sitio) %>%
# summarise(media = mean(ppna, na.rm = TRUE))
# Graficamos
ggplot(cobres_nueva, aes(x = sitio2, y = ppna, fill = sitio)) +
geom_boxplot(
width = 0.4, outliers = F,
show.legend = F) +
geom_point(
size = 2,
width = 0.1,
height = 0,
alpha = 0.5,
position = position_jitter(width = 0.06, seed = 123),
show.legend = F) +
stat_summary(
geom = "point",
fun = "mean",
shape = 23,
size = 3,
fill = "white") +
# Colocamos el texto con geom_text_repel y curvamos la línea de conexión
# geom_text_repel(
# data = medias_ppna,
# aes(x = sitio, y = media, label = round(media, 1)),
# size = 2.5, color = "black", box.padding = 0.5, max.overlaps = 10,
# nudge_x = 0.5, nudge_y = 100,
# segment.linetype = "dashed"
# ) +
labs(
y = expression(paste("PPAN (kg MS·", ha^{-1}, "·", año^{-1})),
x = ""
) +
scale_fill_manual(values = c("#fdae6b", "#a1d99b")) +
scale_y_continuous(
limits = c(0, 2000),
breaks = seq(0, 2000, 500)
) +
theme_bw()
# ggview(width = 3, height = 3)
ggsave("Fig_cajas_medias.png", width = 3.5, height = 3.5, dpi = 600)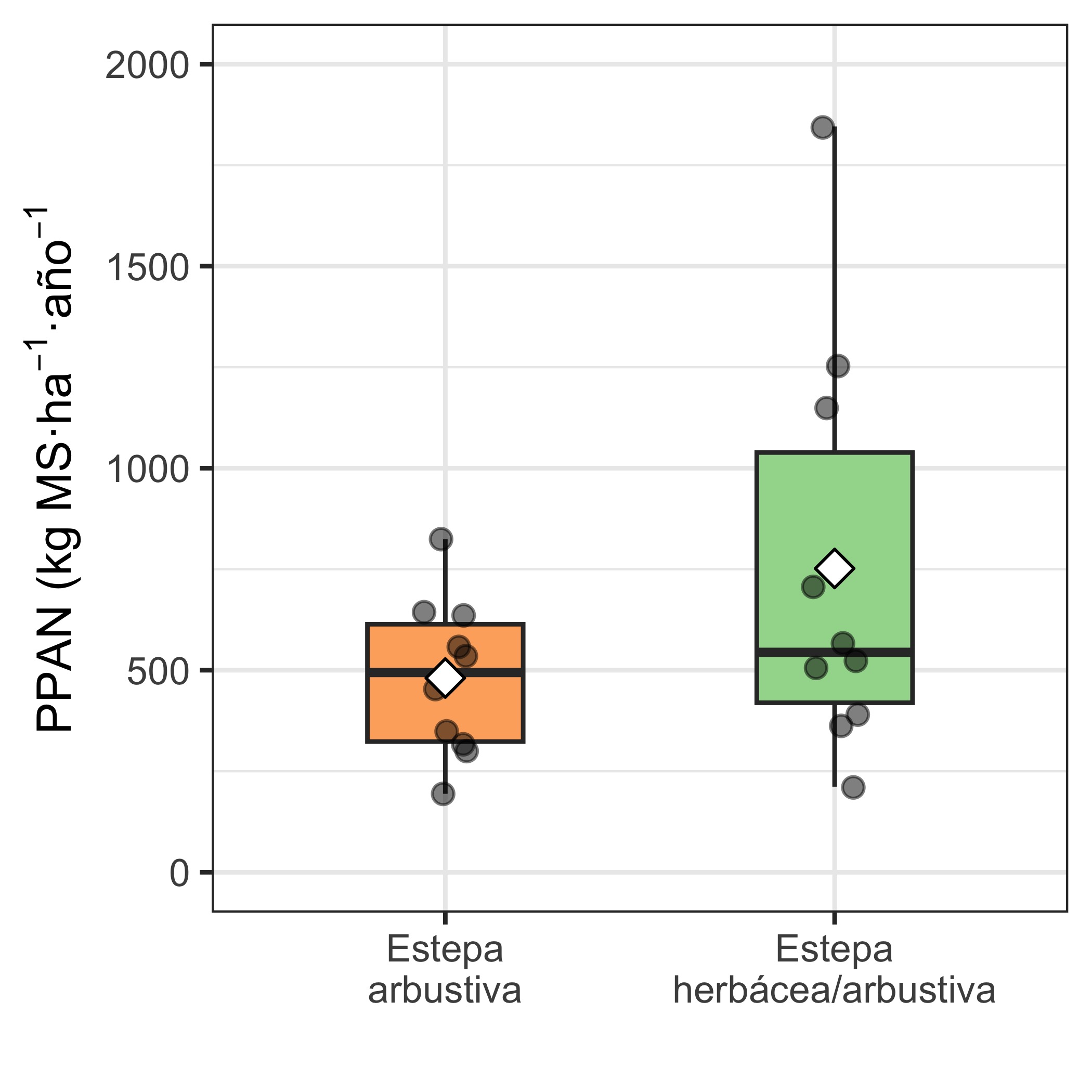
Cuidado…
Ojo, lo se ve en la muestra no necesariamente se lo puede generalizar a la. Para eso es necesario recurrir a la Inferencia Estadística.
2.2 Análisis inferencial
La PPAN promedio en la Estepa herbácea/arbustiva (751.8 kg MS/ha/año ) fue 1.6 veces mayor que en la Estepa arbustiva (480.7 kg MS/ha/año), y esta diferencia fue marginalmente significativa (Tabla 2). También la variabilidad de la PPAN en la Estepa herbácea/arbustiva (CV = 67.7%; Rango: 211.7-1845.7 kg MS/ha/año) fue mayor que en la Estepa arbustiva (CV = 40.3%; Rango: 194.1-824.1 kg MS/ha/año)(Figura 1)(Bartlett’s K-squared = 6.96, df = 1, p = 0.008).
Mostrar el código
# Realiza el análisis y extrae solo el valor t y el valor p
resultado_ttest <- cobres_nueva %>%
select(fecha2, sitio, ppna) %>%
pivot_wider(names_from = sitio, values_from = ppna, names_prefix = "ppna_") %>%
summarize(t_test = list(t.test(ppna_Campo, ppna_Cerro, paired = TRUE, alternative = "less"))) %>%
pull(t_test) %>%
purrr::map_df(~tibble(
estadistico_t = .x$statistic,
p_value = .x$p.value
))
# Crea la tabla elegante con gt
resultado_ttest %>%
gt() %>%
tab_header(
title = "Resultados de la prueba t para muestras apareadas"
) %>%
cols_label(
estadistico_t = "Estadístico t",
p_value = "Valor p"
) %>%
fmt_number(
columns = vars(estadistico_t, p_value),
decimals = 3
)| Resultados de la prueba t para muestras apareadas | |
|---|---|
| Estadístico t | Valor p |
| −1.698 | 0.062 |
Resumiendo la PPAN…
La Estepa herbácea/arbustiva tendió a ser más productivo (diferencia marginalmente significativa) y fue más variable que la Estepa arbustiva.
3 PPAN en los distintos años, por sitio ecológico, y precipitaciones
Creo que de las dos representaciones (Figura 2 y Figura 3), conviene más la Figura 3, ya que no tiene sentido mostrar en paneles separados lo que pasó en Campo y Cerro.
Mostrar el código
cobres_nueva %>%
ggplot(aes(x = fecha2)) +
facet_wrap(~sitio2) +
geom_col(aes(y = ppna, fill = sitio), show.legend = FALSE) +
geom_line(aes(y = precip_gaitan_2 * 9,
group = sitio,
color = "Precipitación"),
size = 0.5) +
scale_y_continuous(
name = expression(paste("PPAN (kg MS·", ha^{-1}, "·", año^{-1})),
limits = c(0, 2000),
sec.axis = sec_axis(~ . / 9, name = "Precipitación (mm)")) +
theme_bw() +
theme(axis.text.x = element_text(angle = 45, hjust = 1, size = 8)) +
labs(
# title = "Con precipitaciones en la estación de crecimiento (GEE)",
x = NULL,
y = expression(PPAN~"(Kg MS / año)")
) +
scale_fill_manual(values = c("#fdae6b", "#a1d99b")) +
scale_color_manual(values = "blue") +
theme(
axis.title.y.left = element_text(color = "black"),
axis.title.y.right = element_text(color = "black"),
legend.position = "bottom"
)
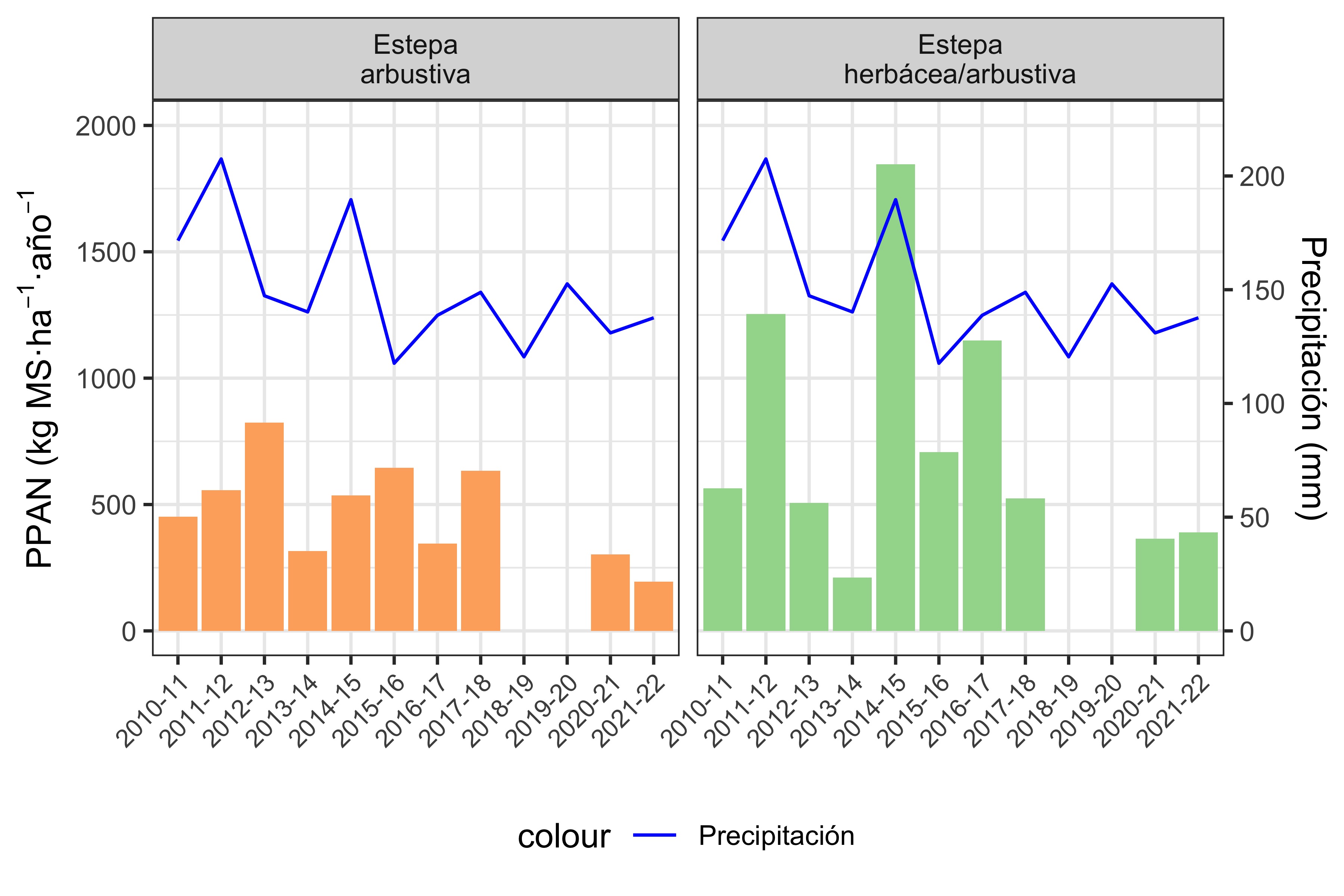
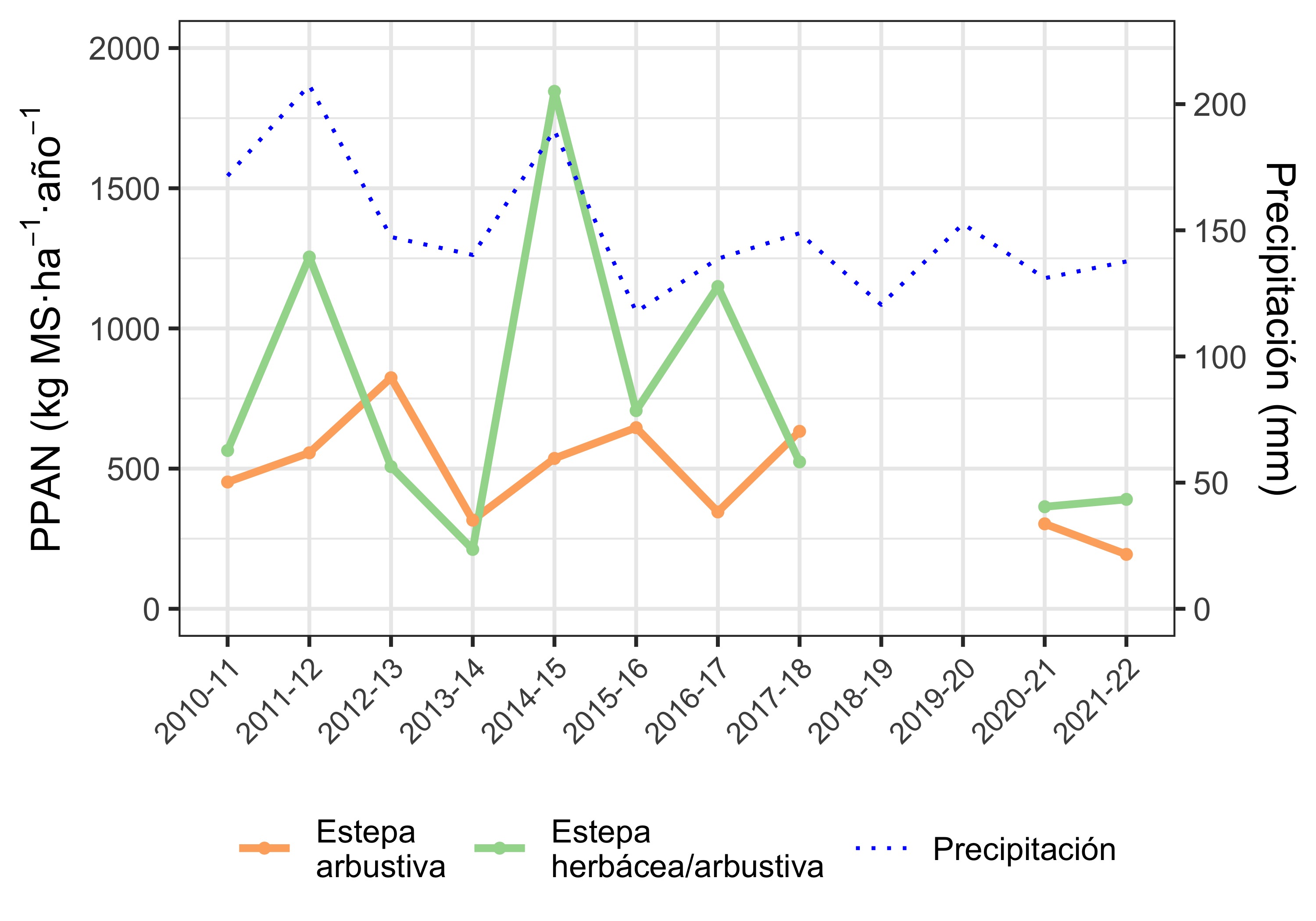
Tal como mencionó Mariana en el grupo de WhatsApp, la respuesta de la PPAN a las lluvias varía según el sitio ecológico, en las muestras analizadas. Se observa que la PPAN de la Estepa herbácea/arbustiva sigue de cerca las precipitaciones de esa estación de crecimiento. En cambio, la respuesta de la Estepa arbustiva está defasada un año, ya que depende de las precipitaciones de la estación de crecimiento del año anterior (Figura 3).
Mostrar el código
cobres_nueva %>%
ggplot(aes(x = fecha2)) +
geom_line(aes(y = ppna, color = sitio2, group = sitio2),
size = 1,
na.rm = TRUE) + # PPAN como línea
geom_point(aes(y = ppna, color = sitio2, group = sitio2),
size = 1,
na.rm = TRUE) + # PPAN como línea
geom_line(
aes(
y = precip_gaitan_2 * 9,
group = sitio,
color = "Precipitación"
),
size = 0.5,
linetype = "dotted"
) + # Precipitaciones como línea
scale_y_continuous(
# name = expression(PPAN ~ "(Kg MS / año)"),
limits = c(0, 2000),
sec.axis = sec_axis(~ . / 9, name = "Precipitación (mm)")) +
theme_bw() +
theme(axis.text.x = element_text(
angle = 45,
hjust = 1,
size = 8
)) +
labs(x = NULL,
y = expression(paste("PPAN (kg MS·", ha^{-1}, "·", año^{-1})),
color = NULL,
# subtitle = "Precipitación de la estación de crecimiento (GEE)"
) +
scale_color_manual(values = c("#fdae6b", "#a1d99b", "blue")) + # Mismos colores que antes, agregando "blue" para Precipitación
theme(
axis.title.y.left = element_text(color = "black"),
axis.title.y.right = element_text(color = "black"),
legend.position = "bottom"
)
Eduardo sugiró que pongamos la barra de error estándar arriba de cada barra (que representa el promedio de las 3 clausuras). Es buena la sugerencia, así que el cambio de gráfico se puede ver en la Figura 4.
Mostrar el código
cobres_nueva %>%
ggplot(aes(x = fecha2, y = ppna, fill = sitio2, group = sitio2)) +
geom_col(position = position_dodge(0.9), na.rm = TRUE) + # Barras de PPNA
geom_errorbar(aes(ymin = ppna, ymax = ppna + ppna_se),
width = 0.1,
position = position_dodge(0.9), na.rm = TRUE, color = "grey50") + # Barras de error alineadas
geom_line(
aes(
y = precip_gaitan_2 * 9,
group = sitio2,
color = "Precipitación"
),
size = 0.5,
linetype = "dotted"
) + # Precipitaciones como línea
scale_y_continuous(
# name = expression(PPAN ~ "(Kg MS / año)"),
limits = c(0, 2500),
sec.axis = sec_axis(~ . / 9, name = "Precipitación (mm)")
) +
theme_bw() +
theme(axis.text.x = element_text(
angle = 45,
hjust = 1,
size = 8
)) +
labs(x = NULL,
y = expression(paste("PPAN (kg MS·", ha^{-1}, "·", año^{-1})),
fill = NULL, color = NULL,
# subtitle = "Precipitación de la estación de crecimiento (GEE)"
) +
scale_fill_manual(values = c("#fdae6b", "#a1d99b")) +
scale_color_manual(values = "blue") +
theme(
axis.title.y.left = element_text(color = "black"),
axis.title.y.right = element_text(color = "black"),
legend.position = "bottom"
)
ggsave("Fig_barras_con_errores.png", width = 5, height = 3.5, dpi = 600)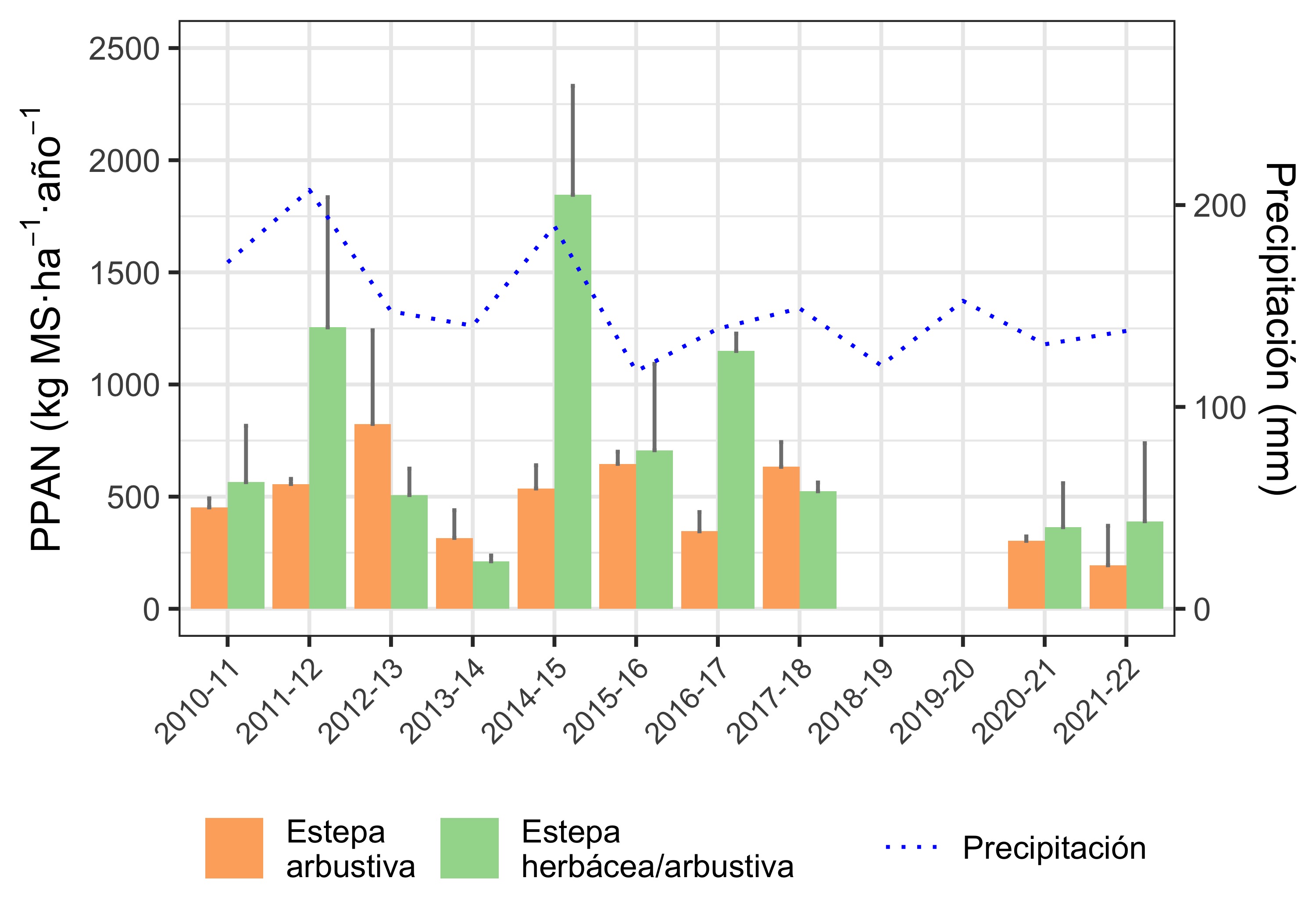
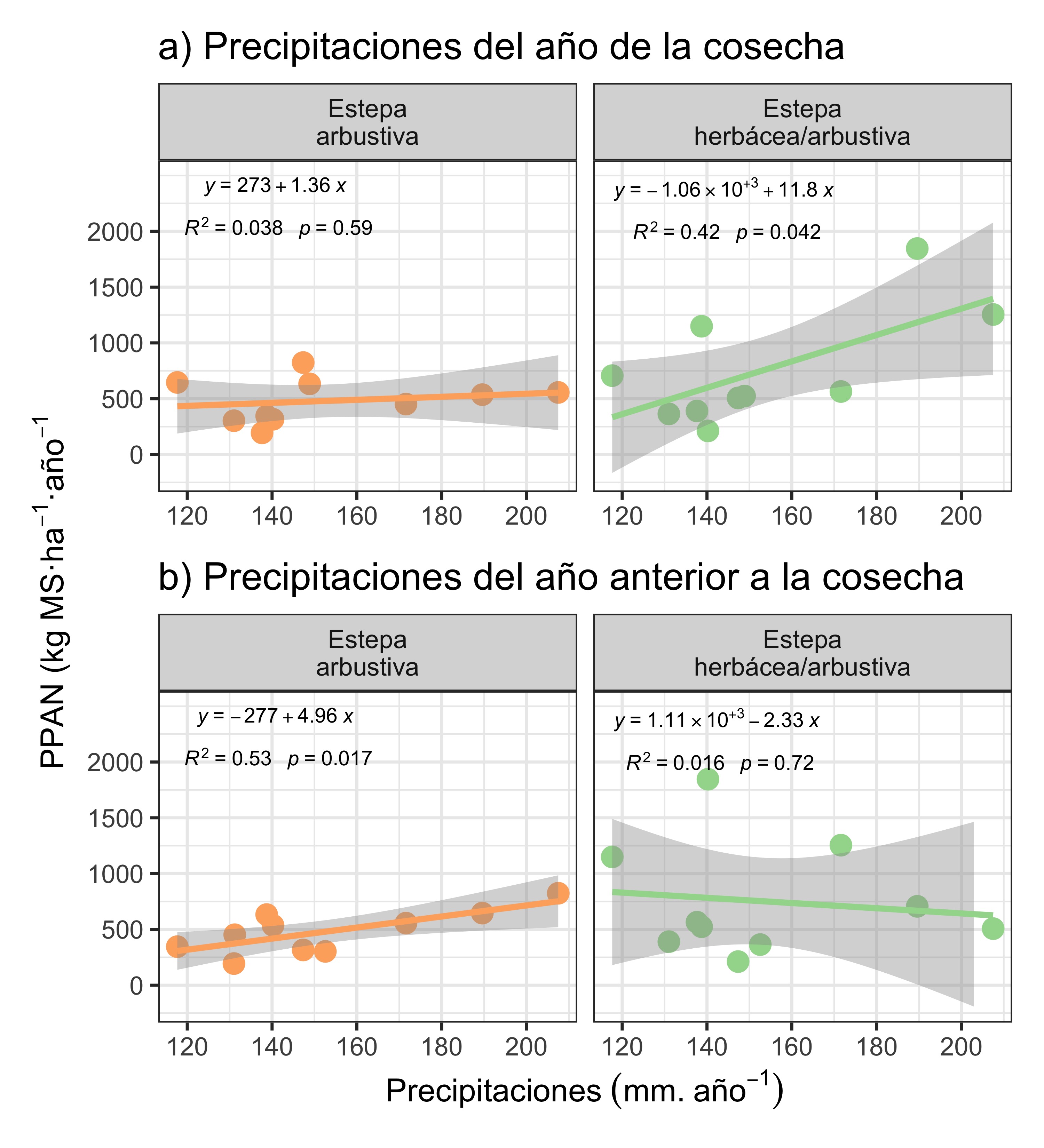
4 Relación entre PPAN y Precipitaciones.
4.1 Análisis descriptivo
Al analizar la relación entre la PPAN y las precipitaciones de la estación de crecimiento del año de cosecha, encontramos que, como se mencionó anteriormente, no hay relación en la Estepa arbustiva. En cambio, para la Estepa herbácea/arbustiva, se observa una clara relación positiva en la muestra analizada. Esto indica que la PPAN depende linealmente de la cantidad de precipitaciones de la estación de crecimiento de ese mismo año en que se estimó la PPAN (Figura 5).
Mostrar el código
cobres_nueva %>%
ggplot(aes(
x = precip_gaitan_2,
y = ppna)
) +
facet_wrap(~sitio2,
# scales = "free_y"
) +
geom_point(aes(color = sitio2),
size = 3,
show.legend = F) +
scale_y_continuous(
# limits = c(0, 2000)
) +
geom_smooth(aes(color = sitio2),
method = "lm",
# se = F,
show.legend = F) +
theme_bw() +
labs(
x = "Precipitaciones en la estación de crecimiento del año de cosecha",
y = expression(paste("PPAN (kg MS·", ha^{-1}, "·", año^{-1}))
) +
scale_color_manual(values = c("#fdae6b", "#a1d99b"))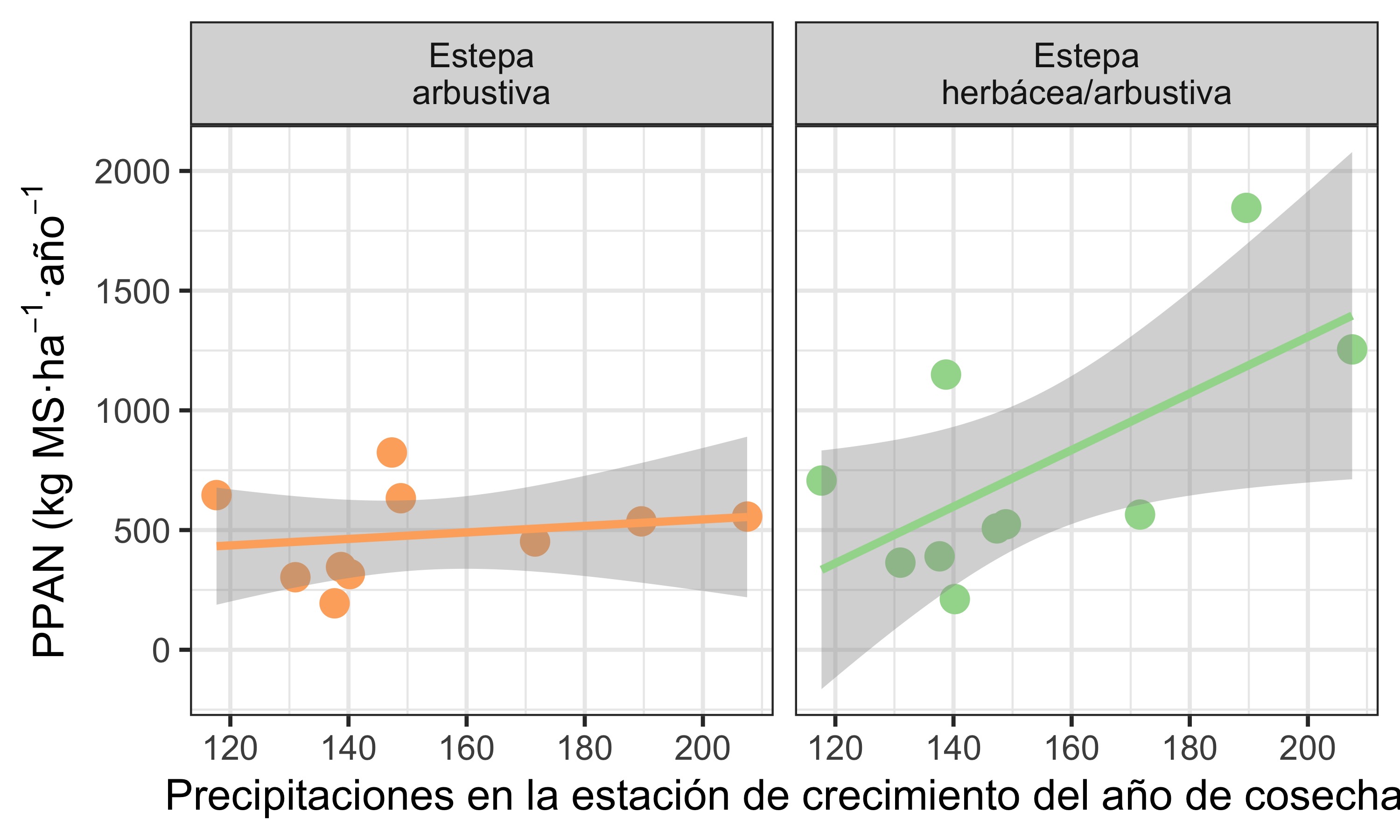
Al explorar la relación con las precipitaciones de la estación de crecimiento del año anterior, el patrón cambia. En la Estepa arbustiva, la relación se vuelve positiva: hay más PPAN cuando llovió más en la estación de crecimiento del año pasado. En cambio, para la Estepa herbácea/arbustiva, no se observa una relación clara (Figura 6).
Mostrar el código
cobres_nueva %>%
ggplot(aes(
x = precip_estacion_anterior_g2,
y = ppna)
) +
facet_wrap(~sitio2,
# scales = "free_y"
) +
geom_point(aes(color = sitio2),
size = 3,
show.legend = F) +
scale_y_continuous(
# limits = c(0, 2000)
) +
geom_smooth(aes(color = sitio2),
method = "lm",
# se = F,
show.legend = F) +
theme_bw() +
labs(
x = "Precipitaciones en la estación de crecimiento del año anterior",
y = expression(paste("PPAN (kg MS·", ha^{-1}, "·", año^{-1}))
) +
scale_color_manual(values = c("#fdae6b", "#a1d99b"))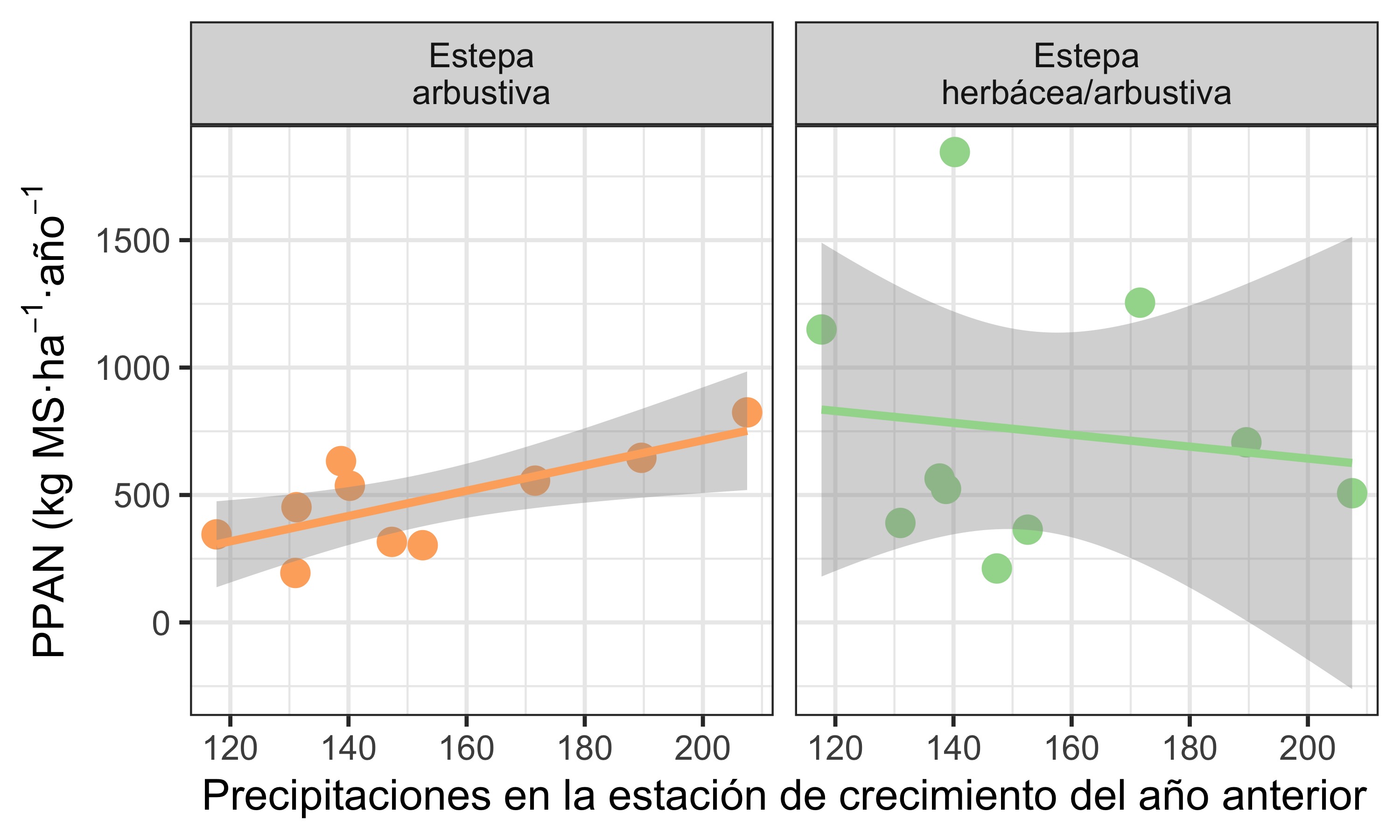
Interesante…
La PPAN de la Estepa herbácea/arbustiva responde a lo que llovió ese mismo año, mientras que la PPAN de la Estepa arbustiva responde a lo que llovió el año pasado.
Hasta aquí, hemos analizado la relación en esta muestra de clauruas y de tiempos. Para determinar si esta tendencia se puede extrapolar a la población, utilizamos la inferencia estadística. Esto se refiere a verificar si la relación fue estadísticamente significativa o no; es importante destacar que “significativo” no siempre implica que sea relevante.
Cuidado…
Ojo, lo se ve en la muestra no necesariamente se lo puede generalizar. Para eso es necesario recurrir a la Inferencia Estadística.
4.2 Análisis inferencial
La relación entre PPAN y precipitaciones en ambos sitios ecológicos es bastante lineal. Por eso, ajusté un modelo de regresión lineal simple para evaluar el ajuste.
Al probar el modelo de la PPAN con las precipitaciones de la estación de crecimiento del año de cosecha, se observa que en la Estepa arbustiva no hay una regresión lineal significativa (b=1.4, P=0.6) (Tabla 3). En cambio, en la Estepa herbácea/arbustiva sí hay una regresión estadísticamente significativa, lo que indica que se puede extrapolar a la población de sitios en la Estepa herbácea/arbustiva (b=12; P=0.042).
La pendiente, que representa el efecto de las precipitaciones de la estación de crecimiento del año de cosecha sobre la PPAN, es positiva. Esto significa que por cada mm de lluvia en la Estepa herbácea/arbustiva, la PPAN aumenta 12 kg MS/ha/año (Tabla 3). Esta cifra es la estimación puntual del efecto de las precipitaciones sobre la PPAN, y el intervalo de confianza del 95% indica que el efecto podría estar entre 0.54 kg MS/ha/año y 23 kg MS/ha/año. El grado de ajuste del modelo es intermedio, con un \(R^2\) de 42.2%.
Mostrar el código
# Ajustar modelos
model_campo <- lm(ppna ~ precip_gaitan_2, data = subset(cobres_nueva, sitio == "Campo"))
model_cerro <- lm(ppna ~ precip_gaitan_2, data = subset(cobres_nueva, sitio == "Cerro"))
# summary(model_campo)
# summary(model_cerro)
# Crear tablas de resumen con R² en notas al pie
tabla_campo <- tbl_regression(model_campo, label = list(precip_gaitan_2 ~ "Precipitación de la estación de ese año")) %>%
modify_header(label ~ "**Predictor**")
tabla_cerro <- tbl_regression(model_cerro, label = list(precip_gaitan_2 ~ "Precipitación de la estación de ese año")) %>%
modify_header(label ~ "**Predictor**")
# Combinar tablas
tabla_merged <- tbl_merge(
tbls = list(tabla_campo, tabla_cerro),
tab_spanner = c("Estepa arbustiva", "Estepa herbáceo/arbustiva")
)
# Agregar R² como fila adicional
# Convertir tabla a objeto gt, si no lo es ya
tabla_gt <- as_gt(tabla_merged)
# Agregar el R² en el encabezado
tabla_gt %>%
tab_header(
title = "Resultados de Modelos",
subtitle = sprintf("R² Campo = %.3f | R² Cerro = %.3f",
summary(model_campo)$r.squared,
summary(model_cerro)$r.squared)
)| Resultados de Modelos | ||||||
|---|---|---|---|---|---|---|
| R² Campo = 0.038 | R² Cerro = 0.422 | ||||||
| Predictor |
Estepa arbustiva
|
Estepa herbáceo/arbustiva
|
||||
| Beta | 95% CI | p-value | Beta | 95% CI | p-value | |
| Precipitación de la estación de ese año | 1.4 | -4.2, 6.9 | 0.6 | 12 | 0.54, 23 | 0.042 |
| Abbreviation: CI = Confidence Interval | ||||||
Cuando probé el ajuste del modelo de la PPAN con las precipitaciones de la estación de crecimiento del año anterior, los resultados se invierten. Para la Estepa arbustiva, sí hay una regresión significativa (b=5.0; P=0.017) (Tabla 4), mientras que para la Estepa herbácea/arbustiva no se puede afirmar que haya una regresión significativa (b=-2.3; P=0.7).
En la Estepa arbustiva, el efecto de las precipitaciones de la estación de crecimiento del año anterior sobre la PPAN es positivo. La interpretación de la pendiente es que por cada mm de lluvia en la Estepa arbustiva, la PPAN aumenta 5 kg MS/ha/año (Tabla 4). Este valor es la estimación puntual del efecto de las precipitaciones sobre la PPAN en la Estepa arbustiva, y el intervalo de confianza del 95% indica que el efecto puede estar entre 1.1 kg MS/ha/año y 8.8 kg MS/ha. De manera similar, el grado de ajuste del modelo es intermedio, con un \(R^2\) de 52.9%.
Mostrar el código
# Ajustar modelos de regresión
model_campo <- lm(ppna ~ precip_estacion_anterior_g2, data = subset(cobres_nueva, sitio == "Campo"))
model_cerro <- lm(ppna ~ precip_estacion_anterior_g2, data = subset(cobres_nueva, sitio == "Cerro"))
# Crear tablas de resumen para cada modelo y cambiar el nombre de precip
tabla_campo <- tbl_regression(model_campo, exponentiate = FALSE,
label = list(precip_estacion_anterior_g2 ~ "Precipitación de la estación del año anterior")) %>%
modify_header(label ~ "**Predictor**")
tabla_cerro <- tbl_regression(model_cerro, exponentiate = FALSE,
label = list(precip_estacion_anterior_g2 ~ "Precipitación de la estación del año anterior")) %>%
modify_header(label ~ "**Predictor**")
# Combinar tablas
tabla_merged <- tbl_merge(
tbls = list(tabla_campo, tabla_cerro),
tab_spanner = c("Estepa arbustiva", "Estepa herbáceo/arbustiva")
)
# Agregar R² como fila adicional
# Convertir tabla a objeto gt, si no lo es ya
tabla_gt <- as_gt(tabla_merged)
# Agregar el R² en el encabezado
tabla_gt %>%
tab_header(
title = "Resultados de Modelos",
subtitle = sprintf("R² Campo = %.3f | R² Cerro = %.3f",
summary(model_campo)$r.squared,
summary(model_cerro)$r.squared)
)| Resultados de Modelos | ||||||
|---|---|---|---|---|---|---|
| R² Campo = 0.529 | R² Cerro = 0.016 | ||||||
| Predictor |
Estepa arbustiva
|
Estepa herbáceo/arbustiva
|
||||
| Beta | 95% CI | p-value | Beta | 95% CI | p-value | |
| Precipitación de la estación del año anterior | 5.0 | 1.1, 8.8 | 0.017 | -2.3 | -17, 12 | 0.7 |
| Abbreviation: CI = Confidence Interval | ||||||
Resumiendo la Estepa herbácea/arbustiva:
La PPAN en la Estepa herbácea/arbustiva responde a lo que llovió en la estación de crecimiento de ese año. Por cada mm de lluvia al año, la PPAN aumenta 12 kg MS/ha/año.
Resumiendo la Estepa arbustiva:
En cambio, la PPAN en la Estepa arbustiva responde a lo que llovió en la estación de crecimiento del año anterior. Por cada mm de lluvia al año, la PPAN aumenta 5 kg MS/ha/año.
5 Unifico las dos figuras de regresión y agrego las ecuaciones
Mostrar el código
fig_reg_1 <-
cobres_nueva %>%
ggplot(aes(x = precip_gaitan_2, y = ppna)) +
facet_wrap(~sitio2) +
geom_point(aes(color = sitio2), size = 3, show.legend = FALSE) +
geom_smooth(aes(color = sitio2), method = "lm", show.legend = FALSE) +
stat_poly_eq(
aes(label = after_stat(
paste(
"atop(",
..eq.label..,
",~italic(R)^2~`=`~", signif(..r.squared.., digits = 2), # Redondeamos R² a 2 decimales
"~~~", expression(italic(p)), "~`=`~", signif(..p.value.., 2), ")"
)
)),
formula = y ~ x,
parse = TRUE,
size = 2.5,
label.y = 0.95
) +
theme_bw() +
labs(
title = "a) Precipitaciones del año de la cosecha",
x = NULL,
y = expression(paste("PPAN (kg MS·", ha^{-1}, "·", año^{-1}))
) +
scale_y_continuous(
limits = c(-200, 2500), breaks = seq(0, 2000, 500)) +
scale_color_manual(values = c("#fdae6b", "#a1d99b"))
fig_reg_2 <-
cobres_nueva %>%
ggplot(aes(
x = precip_estacion_anterior_g2,
y = ppna)
) +
facet_wrap(~sitio2,
# scales = "free_y"
) +
geom_point(aes(color = sitio2),
size = 3,
show.legend = F) +
scale_y_continuous(
# limits = c(0, 2000)
) +
geom_smooth(aes(color = sitio2),
method = "lm",
# se = F,
show.legend = F) +
stat_poly_eq(
aes(label = after_stat(
paste(
"atop(",
..eq.label..,
",~italic(R)^2~`=`~", signif(..r.squared.., digits = 2), # Redondeamos R² a 2 decimales
"~~~", expression(italic(p)), "~`=`~", signif(..p.value.., 2), ")"
)
)),
formula = y ~ x,
parse = TRUE,
size = 2.5,
label.y = 0.95
) +
theme_bw() +
labs(
title = "b) Precipitaciones del año anterior a la cosecha",
x = expression("Precipitaciones" ~ (mm.~año^-1)),
y = expression(paste("PPAN (kg MS·", ha^{-1}, "·", año^{-1}))
) +
scale_y_continuous(
limits = c(-200, 2500), breaks = seq(0, 2000, 500)) +
scale_color_manual(values = c("#fdae6b", "#a1d99b"))
fig_reg_1 / fig_reg_2 +
plot_layout(guides = "collect", axis_titles = "collect")
ggsave("Fig_regresiones_juntas.png", width = 5, height = 5.5, dpi = 600)